🧗‍♂️Random Restart

Recent Notes

MNIST Image Classification with Keras

10 min read

Intro

MNIST Image Classification with Keras Open In Colab

Train a neural network using Keras to classify handwritten digits (0–9) from the MNIST dataset.

description

1. Setup

import tensorflow as tf
import tensorflow_datasets as tfds
from matplotlib import pyplot as plt
import numpy as np

2. Load the MNIST Dataset

# Tuples of uint8 NumPy arrays
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
 
print("Training set:", x_train.shape, y_train.shape)
print("Test set:", x_test.shape, y_test.shape)

3. Visualize Sample Images

print(f"dtype: {x_train[0].dtype}, shape: {x_train[0].shape}")
print(x_train[0])
plt.imshow(x_train[0], cmap='gray')
plt.figure(figsize=(6,6))
for i in range(9):
    plt.subplot(3, 3, i + 1)
    plt.imshow(x_train[i], cmap="gray")
    plt.title(f"Label: {y_train[i]}")
    plt.axis("off")
plt.tight_layout()
plt.show()

4. Preprocess the Data

Transform the dataset into a format suitable for the neural network

Flatten the images

Reshape each image into a flat vector: (28, 28) → (784,)

.

x_train = x_train.reshape(60000, 784)
x_test = x_test.reshape(10000, 784)
print("Training set:", x_train.shape, y_train.shape)
print("Test set:", x_test.shape, y_test.shape)
Training set: (60000, 784) (60000,)
Test set: (10000, 784) (10000,)

Normalize the pixel values

  • X_train = X_train.astype(‘float32’): Convert the training images to float32 type.
  • X_test = X_test.astype(‘float32’): Convert the test images to float32 type.
  • X_train /= 255: Normalize the training images’ pixel values to the range [0, 1].
  • X_test /= 255: Normalize the test images’ pixel values to the range [0, 1].
x_train = x_train.astype('float32') / 255 # uint8 → float32
x_test = x_test.astype('float32') / 255
# print(x_train[0])

One-hot encode labels

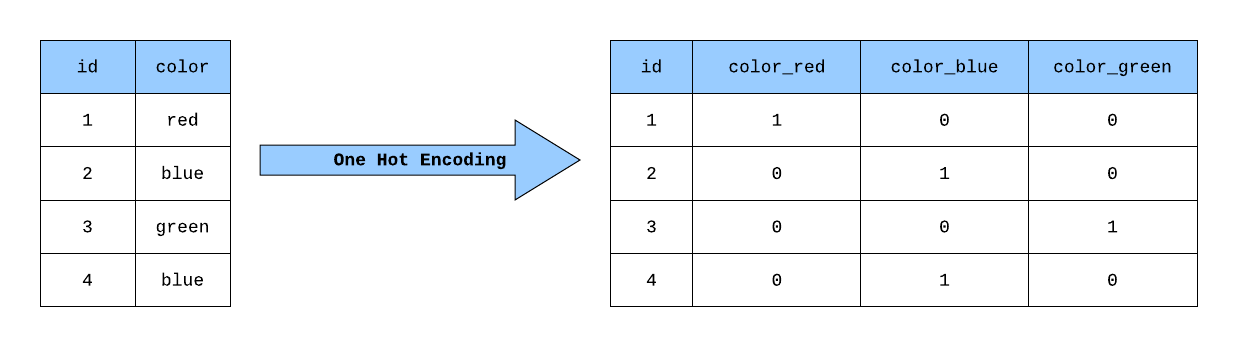
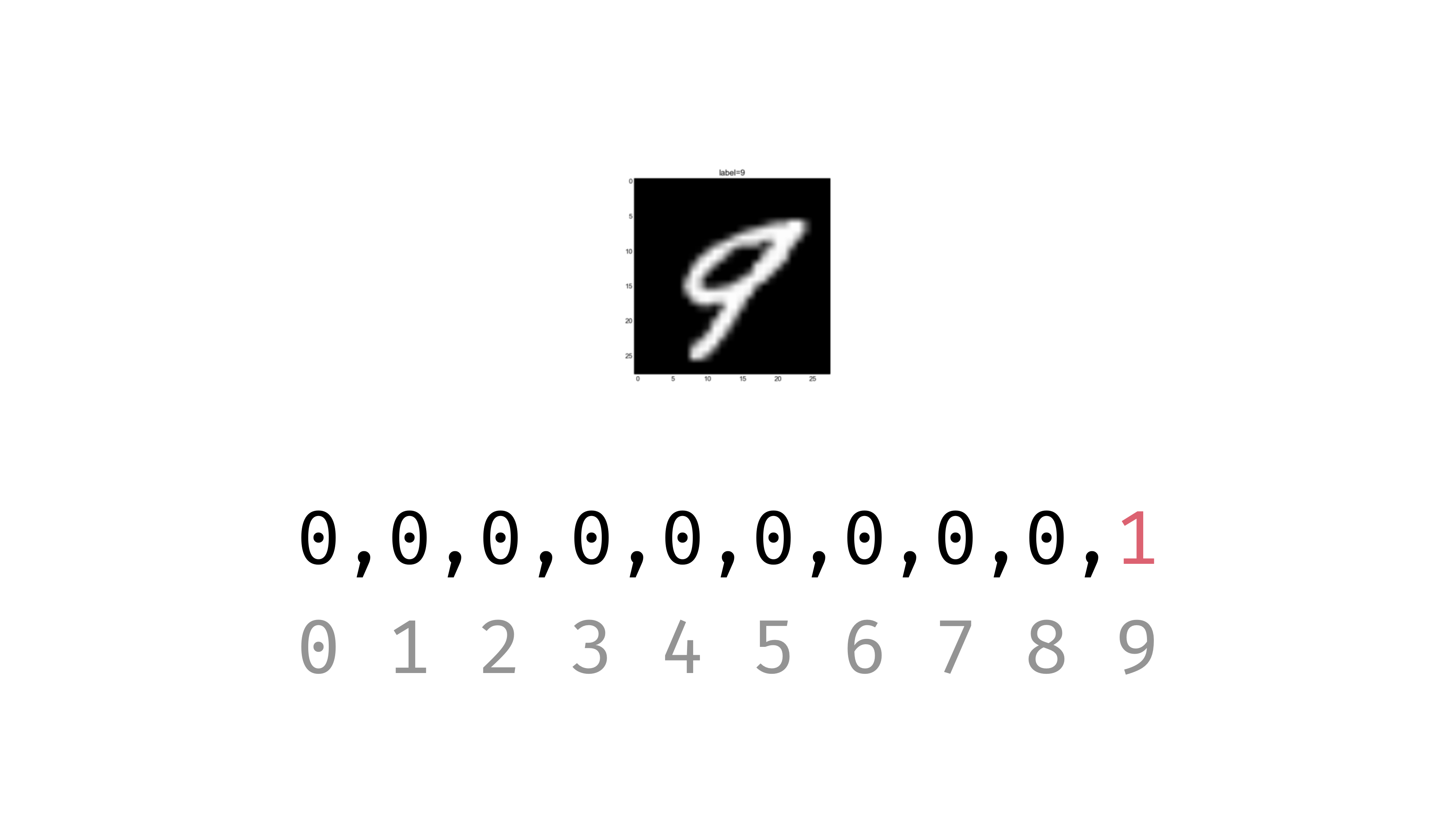
  • Integer labels → One-hot vectors → Output layer neurons
  • Use tf.keras.utils.to_categorical to convert integer labels into one-hot vectors, where the correct class is 1 and all others are 0

One hot encoding example

https://towardsdatascience.com/building-a-one-hot-encoding-layer-with-tensorflow-f907d686bf39

https://codecraft.tv/courses/tensorflowjs/neural-networks/mnist-training-data/

https://stackoverflow.com/questions/33720331/mnist-for-ml-beginners-why-is-one-hot-vector-length-11

n_classes = 10
y_train = tf.keras.utils.to_categorical(y_train, n_classes)
y_test = tf.keras.utils.to_categorical(y_test, n_classes)
print(f'y_train[0]: {y_train[0]}')
y_train[0]: [0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]

5. Build the model

Define the architecture: layers, activations, dropouts, etc.

model = tf.keras.Sequential([
    tf.keras.layers.Dense(512, input_shape=(784,)), # Input: flattened 28x28 vector, Hidden layer: 512 neurons
    tf.keras.layers.Activation('relu'), # ReLU activation to introduce non-linearity
    tf.keras.layers.Dropout(0.2), # Dropout (20%) for regularization to prevent overfitting
    tf.keras.layers.Dense(10), # Output layer: 10 neurons, one per class
    tf.keras.layers.Activation('softmax') # Convert output to probabilities out of 1
])
 
model.summary()
Model: "sequential"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ dense (Dense)                   │ (None, 512)            │       401,920 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ activation (Activation)         │ (None, 512)            │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dropout (Dropout)               │ (None, 512)            │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_1 (Dense)                 │ (None, 10)             │         5,130 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ activation_1 (Activation)       │ (None, 10)             │             0 │
└─────────────────────────────────┴────────────────────────┴───────────────┘
 Total params: 407,050 (1.55 MB)
 Trainable params: 407,050 (1.55 MB)
 Non-trainable params: 0 (0.00 B)

Input: Flattened 28x28 image (784)
          │
          ▼
Dense Layer (512 neurons)
  Activation: ReLU
  Dropout: 0.2
  Params: 401,920
          │
          ▼
Dense Layer (10 neurons)
  Activation: Softmax
  Params: 5,130
          │
          ▼
Output: Probability distribution over 10 classes (digits 0–9)

6. Compile the Model

Configure how the model learns by specifying the loss function, optimizer, and metrics

  • loss='categorical_crossentropy':- Specific implementation of Cross-entropy for multi-class classification problems with one-hot encoded labels
  • optimizer='adam':- adjust model weights efficiently during training
  • metrics=['accuracy']:- tracks the model’s performance during training and testing.
model.compile(
    loss="categorical_crossentropy",
    optimizer="adam",
    metrics=["accuracy"]
)

7. Train the Model

This step starts the Neural Network Training process, where the model learns patterns from the training data (x_train, y_train).

  • The network adjusts its weights using the Adam optimizer to minimize the categorical cross-entropy loss
  • Validation data (x_test, y_test) helps track performance and detect overfitting
  • Training occurs over a number of epochs, and each epoch processes the data in batches
history = model.fit(
    x_train, y_train,
    validation_split=0.1,  # 10% of training data used for validation
    epochs=5,              # Number of times to iterate over the data
    batch_size=128         # Number of samples per weight update
)
Epoch 1/4
469/469 ━━━━━━━━━━━━━━━━━━━━ 9s 17ms/step - accuracy: 0.8626 - loss: 0.4805 - val_accuracy: 0.9559 - val_loss: 0.1465
Epoch 2/4
469/469 ━━━━━━━━━━━━━━━━━━━━ 6s 14ms/step - accuracy: 0.9609 - loss: 0.1342 - val_accuracy: 0.9692 - val_loss: 0.1025
Epoch 3/4
469/469 ━━━━━━━━━━━━━━━━━━━━ 10s 13ms/step - accuracy: 0.9733 - loss: 0.0904 - val_accuracy: 0.9762 - val_loss: 0.0770
Epoch 4/4
469/469 ━━━━━━━━━━━━━━━━━━━━ 7s 15ms/step - accuracy: 0.9808 - loss: 0.0645 - val_accuracy: 0.9782 - val_loss: 0.0707
<keras.src.callbacks.history.History at 0x781c8c59ebd0>
  • The history object stores the loss and accuracy at each epoch, which can later be plotted to visualize training progress.

8. Evaluate on the Test Set

Measure final performance on test set

  • Evaluates the trained neural network model on the test data (X_test and Y_test) and prints out the test score (loss) and test accuracy
score = model.evaluate(x_test, y_test, verbose=0)
# print(score)
print('Test score:', score[0])
print('Test accuracy:', score[1])

Plot Training History

Visualizes model learning and convergence

plt.plot(history.history['accuracy'], label='train')
plt.plot(history.history['val_accuracy'], label='val')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()
plt.show()

9. Prediction

  • Predict labels for test data
predictions = model.predict(x_test)
print(predictions[0])
 
# Convert probabilities into actual class labels
predicted_classes = np.argmax(predictions, axis=-1)
print(predicted_classes[0])
 
# Show a few predictions
y_test = np.argmax(y_test, axis=-1)
correct_indices = np.nonzero(predicted_classes == y_test)[0]
incorrect_indices = np.nonzero(predicted_classes != y_test)[0]
plt.figure()
for i, correct in enumerate(correct_indices[:9]):
    plt.subplot(3,3,i+1)
    plt.imshow(x_test[correct].reshape(28,28), cmap='gray', interpolation='none') # reshape image for plotting
    plt.title("Predicted {}, Class {}".format(predicted_classes[correct], y_test[correct]))
plt.tight_layout()
313/313 ━━━━━━━━━━━━━━━━━━━━ 2s 7ms/step
[4.7690773e-06 6.0700955e-08 6.1652237e-05 4.6185945e-04 3.4014103e-09
 5.3657391e-07 1.8727768e-10 9.9943292e-01 1.3097859e-05 2.5006822e-05]
7

Graph View